Theorie zu musikalischen Stimmungen
Der Einzelton
Der Einzelton ist eine einfache Schwingung, die durch ihre Frequenz (Anzahl Schwingungen pro Sekunde) in der Masseinheit Herz (Hz.) und durch die Lautstärke definiert ist. In der Praxis ist ein Ton meistens von mitschwingenden Obertönen begleitet, die den Ton in ihrem Klang charakterisieren. So ist der Ton einer Flöte zum Ton einer Trompete durch diese Obertöne in ihrer Klangfarbe markant unterschiedlich.
Die Intervalle
Zwei Töne, die miteinander schwingen, erregen unser Empfinden
und wir unterscheiden Intervalle, die sehr harmonisch klingen von denen, die
weniger gut klingen und solche, die sich derart reiben, dass wir sie als
unangenehm empfinden. Es ist die Kunst der Musik, durch gezielte Wahl der
Intervalle unsere Gefühle an verschiedenen Stellen zu berühren. Fast alle
namhaften Mathematiker haben sich mit der Theorie der Harmonielehre beschäftigt.
Euler hat einen Massstab zur Klassifizierung von Intervallen in Konsonanzgrade
aufgestellt. Die nachstehenden Intervalle mit ihren Frequenzverhältnissen
gelten klassifiziert als harmonisch.
Konsonanzgrade diverser Intervalle in der reinen Stimmung
| Intervalle | Frequenzverhältnisse | Konsonanzgrade |
| Prim | 1:1 | 1 |
| Oktave | 1:2 | 2 |
| Duodezime | 1:3 | 3 |
| Zwei Oktaven | 1:4 | 3 |
| Quinte | 2:3 | 4 |
| Zwei Duodezimen | 1:6 | 4 |
| Drei Oktaven | 1:8 | 4 |
| Quarte | 3:4 | 5 |
Die Tonleiter
In der westlichen Welt hat sich durchgesetzt, die Oktave in 12 Halbtonschritte aufzuteilen (chromatische Tonleiter). Dabei ist es möglich, die Oktave mit 12 gleichen Halbtonschritten (gleichstufige Stimmung) oder mit 12 ungleich grossen Halbtonschritten (ungleichstufige Stimmung) zu durchlaufen. Jede dieser Möglichkeiten führt zu einem unterschiedlichen Klang.
Die ungleichstufige Stimmung
Aus den vielen möglichen Varianten ungleichstufiger Stimmungen
wollen wir die wichtigste, die reine Stimmung herausgreifen. Gemäss
nachfolgender Aufstellung stehen die 12 Halbtöne einer Oktave in einem festen
Frequenzverhältnis zum Grundton (f0). Die Frequenz des n-ten
Halbtons wird mit fn bezeichnet.
Das Frequenzverhältnis der Halbtonintervalle zum Grundton in der reinen
Stimmung
| Frequenz des Halbtons | Tonschritt |
| f0 = 1 · f0 | Prim |
| f1 = 16/15 · f0 | Kleine Sekund |
| f2 = 9/8 · f0 | Grosse Sekund |
| f3 = 6/5 · f0 | Kleine Terz |
| f4 = 5/4 · f0 | Grosse Terz |
| f5 = 4/3 · f0 | Quarte |
| f6 = 45/32 · f0 | Tritonus |
| f7 = 3/2 · f0 | Quinte |
| f8 = 8/5 · f0 | Kleine Sext |
| f9 = 5/3 · f0 | Grosse Sext |
| f10 = 9/5 · f0 | Keine Septime |
| f11 = 15/8 · f0 | Grosse Septime |
| f12 = 2 · f0 | Oktave |
Die Durtonleitern der reinen Stimmung
Das feste Frequenzverhältnis der 12 Halbtöne einer Oktave zum
Grundton ist relativ. Auf jedem Grundton mit einer beliebigen Frequenz kann
demzufolge eine Durtonleiter in reiner Stimmung aufgebaut werden. Erst mit dem
Referenzton (Kammerton) wird die Tonskala mit absoluten Frequenzzahlen
definiert. Es hat sich durchgesetzt, dass die Frequenz des Tones a der
eingestrichenen Oktave mit 440 Herz festgelegt ist und dass auf jedem Halbton
eine neue Durtonleiter (Tonart) aufgebaut wird. Somit sind 12 Durtonarten möglich.
Mit dem Quintenzirkel werden sechs # -Tonarten von C nach oben schreitend und
sechs b-Tonarten von C nach unten schreitend definiert. Oft fühlen sich Musiker
in diesem Tonartenraster eingeengt und variieren den Referenzton (Kammerton) in
seiner Frequenz beliebig nach unten oder nach oben.
Die Frequenzen aller Halbtöne in den 12 reinen Durtonarten
| Ton / Tonart |
c | cis des |
d | dis es |
e | f | fis ges |
g | gis as |
a | ais b |
h | c |
| c-Dur | 264 | 281.6 | 297.0 | 316.8 | 330 | 352 | 371.3 | 396 | 422.4 | 440 | 475.2 | 495 | 528 |
| des-Dur | 257.8 | 275 | 293.3 | 309.4 | 330 | 343.8 | 366.7 | 386.7 | 412.5 | 440 | 458.3 | 495 | 515.6 |
| d-Dur | 264 | 275 | 293.3 | 312.9 | 330 | 352 | 366.7 | 391.1 | 412.5 | 440 | 469.3 | 488.9 | 528 |
| es-Dur | 260.7 | 281.6 | 293.3 | 312.9 | 333.7 | 352 | 375.5 | 391.1 | 417.2 | 440 | 469.3 | 500.6 | 521.5 |
| e-Dur | 264 | 275 | 297 | 309.4 | 330 | 352 | 371.3 | 396 | 412.5 | 440 | 464.1 | 495 | 528 |
| f-Dur | 264 | 281.6 | 293.3 | 316.8 | 330 | 352 | 375.5 | 396 | 422.4 | 440 | 469.3 | 495 | 528 |
| fis-Dur | 257.8 | 275 | 293.3 | 305.6 | 330 | 343.8 | 366.7 | 391.1 | 412.5 | 440 | 458.3 | 488.9 | 515.6 |
| ges-Dur | 257.8 | 275 | 293.3 | 305.6 | 330 | 343.8 | 366.7 | 391.1 | 412.5 | 440 | 458.3 | 488.9 | 515.6 |
| g-Dur | 260.7 | 275 | 293.3 | 312.9 | 325.9 | 352 | 366.7 | 391.1 | 417.2 | 440 | 469.3 | 488.9 | 521.5 |
| as-Dur | 257.8 | 275 | 290 | 309.4 | 330 | 343.7 | 371.2 | 386.7 | 412.5 | 440 | 464.1 | 495 | 515.6 |
| a-Dur | 264 | 275 | 293.3 | 309.4 | 330 | 352 | 366.7 | 396 | 412.5 | 440 | 469.3 | 495 | 528 |
| b-Dur | 264 | 281.6 | 293.3 | 312.9 | 330.0 | 352 | 375.5 | 391.1 | 422.4 | 440 | 469.3 | 500.6 | 528 |
| h-Dur | 260.7 | 275 | 293.3 | 305.6 | 325.9 | 343.8 | 366.7 | 391.1 | 407.4 | 440 | 458.3 | 488.9 | 521.5 |
Die absoluten Frequenzwerte der einzelnen Töne in der Tabelle der chromatischen Durtonleitern zeigen, dass der Wechsel in eine andere Tonart die Umstimmung gewisser Töne fordert. Es gäbe sonst Intervalle, die heulende Dissonanzen hervorbringen wie z.B. die Wolfsquinte. Bei fest gestimmten Musikinstrumenten ist dies nicht möglich. So hat man sich z.B. bei Kirchenorgeln mit mehreren Manuals beholfen, die auf unterschiedlich gestimmte Register zugriffen.
Das Pythagoräische Komma
Schon der Mathematiker Pythagoras hat vor über 2000 Jahren
erkannt, dass die Aneinanderreihung reiner Intervalle zu einer Abdrift der
Tonart führt. Dieses Phänomen lässt sich mit folgendem Beispiel belegen:
Das Intervall einer reinen Quinte hat das Frequenzverhältnis 1:3/2. Zwölf
Quinten sind zusammen 12 · 7 = 84 Halbtöne. Sieben Oktaven zusammen sind
ebenfalls 7 · 12 = 84 Halbtöne. Werden vom Ausgangston mit der Frequenz f0
z.B. 12 Qinten aufwärts-schreitend aneinandergereiht und vom erreichten Endton
wieder 7 Oktaven nach unten-schreitend aneinandergereiht, so könnte man
glauben, wieder am Anfangston mit der Frequenz f0 zu sein. Wie die
folgende Formel belegt, ist der Schlusston nicht genau die Frequenz f0
sondern 1.0136 · f0
![]()
Diese Abweichung nennt man das Pythagoräische Komma. Die Komplexität der Zusammenhänge in der Harmonielehre hat zu einem Kompromiss geführt, damit auf einer Tastatur (Klavier) alle Tonarten gespielt werden können. Es wird Bach zugeschrieben, die wohl temperierte Stimmung erfunden zu haben. Heute hat sich die gleichstufig temperierte Stimmung auf der Basis der reinen Oktave als Normstimmung durchgesetzt.
Die gleichstufig temperierte Stimmung auf der Basis der reinen Oktave
Es liegt nahe, die Oktave in mathematisch 12 gleiche Halbtonstufen zu unterteilen. Dabei ist jeder Halbton von seinem benachbarten Halbton in seiner Frequenz um einen konstanten Faktor U distanziert. 12 Halbtöne ergeben somit das Frequenzverhältnis 1:2 der Oktave. Somit ist der Halbtonschritt
![]()
In dieser Stimmung sind alle Intervalle ausser der Oktave geringfügig unrein. Der Vorteil liegt darin, dass alle Tonarten auf einer Tastatur spielbar sind.
Die absoluten Frequenzen aller Halbtöne der 12 Durtonarten in der gleichstufig temperierten Stimmung auf der Basis der reinen Oktave
| Ton / Tonart |
c | cis des |
d | dis es |
e | f | fis ges |
g | gis as |
a | ais b |
h | c |
| c-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| des-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| d-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| es-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| e-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| f-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| fis-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| ges-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| g-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| as-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| a-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| b-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
| h-Dur | 261,6 | 277,2 | 293,7 | 311,1 | 329,6 | 349,2 | 370 | 392 | 415,3 | 440 | 466,2 | 493,9 | 523,2 |
So ideal diese gleichstufig temperierte Stimmung auf der Basis der reinen Oktaven erscheinen mag, bleibt sie trotzdem eine Kompromisslösung. Die Terzen sind dominant unrein und auch andere Intervalle klingen durch Schwebungen in den Obertönen rauh. Dem Wechsel in eine andere Tonart fehlt die spezifische Klangfarbe. Die Tonarten klingen alle gleich. Es ist den vielen strebsamen Musikern und Instrumentenstimmern zu verdanken, dass sie nach Möglichkeiten zur Klangoptimierung gesucht und Lösungen dazu gefunden haben.
Die Streckung der Oktave
Besonders beim Klavier ist festzustellen, dass die Obertöne leicht erhöht sind und dadurch der Klang merklich beeinflusst wird. Dieses Phänomen lässt sich durch die Steifigkeit der Saiten erklären, die sich an ihren Einspannstellen nicht widerstandslos bewegen können und dadurch die Saitenlängen faktisch verkürzen. Dabei spricht man von einer natürlichen Streckung. Es ist auch möglich, die Oktave gezielt zu strecken. Viele Versuche haben gezeigt, dass sich der Klang dadurch deutlich optimieren lässt. Über das Mass der Streckung lässt sich philosophieren. Erfahrungsgemäss bringen Oktavstreckungen zwischen 1 und 3 Cent sehr gute Resultate.
Gleichstufig gestreckte temperierte Stimmung auf der Basis der reinen Quinte
Schon Pythagoras hat versucht, reine Quinten aneinander zu reihen. Dadurch wird die Oktave gestreckt. Das Intervall einer Quinte hat das Frequenzverhältnis 1: 3/2 und besteht aus 7 Halbtönen. Wird die Quinte mathematisch gleichstufig aufgeteilt, so erhalten wir den Faktor V, um den sich die nebeneinander liegenden Halbtöne unterscheiden. Somit ist der Halbtonschritt
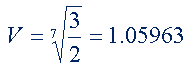
In dieser Stimmung sind alle Halbtöne leicht verstimmt ausser der Quinte. Es zeigt sich, dass Intervalle, die mehrere Oktaven überspannen, unrein klingen. Alle Tonarten sind auf einer Tastatur spielbar.
Die Frequenzen aller Halbtöne der 12 Durtonarten in der gleichstufig gestreckten temperierten Stimmung auf der Basis der reinen Quinte.
| Ton / Tonart |
c | cis des |
d | dis es |
e | f | fis ges |
g | gis as |
a | ais b |
h | c |
| c-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| des-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| d-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| es-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| e-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| f-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| fis-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| ges-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| g-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| as-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| a-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| b-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
| h-Dur | 261,2 | 276,8 | 293.3 | 310,8 | 329,4 | 349 | 369,8 | 391,9 | 415,2 | 440 | 466,2 | 494 | 523,9 |
Die Masseinheit Cent
Um die Abweichung eines Tones von seinem Sollwert massstäblich darzustellen, wurde das Centmass eingeführt. Dabei wird die Oktave in 1200 Cent unterteilt. Ein gleichstufiger Halbtonschritt auf der Basis einer reinen Oktave hat somit 100 Cent. Mit diesem sehr feinen Massstab lässt sich die Präzision einer Stimmung physikalisch genau darstellen.
Schlussbemerkung
Töne und Intervalle präzise zu stimmen ist aufgrund der
Komplexität der Harmonie sehr schwierig. Jeder Eingriff hat Auswirkungen auf
den gesamten Zusammenhang der Intervalle. Besonders die gleichstufigen
Stimmungen (Oktavstreckungen etc.) sind mit dem menschlichen Hörorgan nur sehr
schwer zu bewerkstelligen. Wenn auch Verfahren (wie Kirnberger etc.) beim
Stimmen angewendet werden, ist es sehr schwierig, die kleinen Unterschiede in
den Schwebungen der Töne zu beurteilen. Es ist für Instrumentenstimmer absolut
zielführender und rationeller, ein präzises Stimmgerät zu verwenden. Damit
kann unzweifelhaft die Abweichung der Stimmung festgestellt werden.
Das Stimmgerät Instrument-Tuner
der Firma NetCat AG erfüllt diese Anforderungen perfekt und kann direkt auf
verschiedene Stimmungen eingestellt werden. Die Stimmung, der Grundton, der
Referenzton, die Kalibration sowie die Oktavstreckung können zudem variiert
werden. Zusätzlich können eigene Stimmungen erstellt und in die Auswahl der
Stimmungen eingefügt werden. Dieses präzise Stimmgerät zeichnet sich auch
durch eine hervorragende Bedienerfreundlichkeit und durch die automatische
Protokollierung aus. Eine schriftliche Protokollierung der Stimmung gilt heute
als unerlässliches Zertifikat der Qualität. Eine kostenlose Versuchsversion
der Software kann unter http://www.instrument-tuner.com
heruntergeladen werden.